부분집합

부분집합의 수

• 집합의 원소가 n개일 때, 공집합을 포함한 부분집합의 수는 2^n개이다.
• 이는 각 원소를 부분집합에 포함시키거나 포함시키지 않는 2가지 경우를 모든 원소에 적용한 경우의 수와 같다

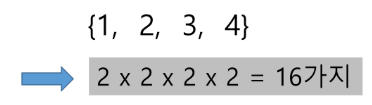
반복문을 이용한 부분집합 구하기

package day0321_부분집합_조합;

import java.util.Arrays;

public class 부분집합_1 {
	String[] 재료 = {"참치", "우엉", "삼겹살"};
	public static void main(String[] args) {
		//반복문을 이용해서 부분집합을 구해보자.
		int N = 3;
		int[] sel = new int[N];
		
		for(int i = 0 ; i<2; i++) {
			sel[0] = i;
			for(int j = 0; j<2; j++	) {
				sel[1] = j;
				for(int k = 0 ; k<2; k++) {
					sel[2] = k;
					System.out.println(Arrays.toString(sel));
				}
			}
		}
	}
}
//
[0, 0, 0]
[0, 0, 1]
[0, 1, 0]
[0, 1, 1]
[1, 0, 0]
[1, 0, 1]
[1, 1, 0]
[1, 1, 1]

비트마스킹을 이용한 부분집합 구하기

package day0321_부분집합_조합;

public class 부분집합_2 {
	static String[] 재료 = {"참치", "우엉", "삼겹살"};
	public static void main(String[] args) {
		//비트마스킹을 이용해보자
		int N = 3;
		
		//i는 모든 부분집합을 의미한다.
		for(int i = 0 ; i<(1<<N); i++) {
			//i가 부분집합 중 1개라는 것은 알겠어.
			//그런데 i가 무슨 원소를 가진 부분집합인지는 몰라
			//i가 무슨 원소를 가진 부분집합인지 검사를 해야해.
			//N개의 원소를 검사를 한다.
			String tmp = "";
			for(int j = 0 ; j < N; j++) {
				//i의 j번째 비트에 해당 값이 있는지 쳌
//				if((i & (1<<j)) != 0) {
				if((i & (1<<j)) > 0) {
					//해당 j번째의 요소가 이번 부분집합에는 포함되어 있습니다.
					tmp+=재료[j];
				}
			}
			System.out.println(tmp);
		}
	}
}
//
(충무김밥)
참치
우엉
참치우엉
삼겹살
참치삼겹살
우엉삼겹살
참치우엉삼겹살

재귀를 이용한 부분집합

package day0321_부분집합_조합;

public class 부분집합_3 {
	static String[] 재료 = {"참치", "우엉", "삼겹살"};
	static int N;
	static boolean[] sel ; //해당 요소 선택 했다!
	
	public static void main(String[] args) {
		N = 3;
		sel = new boolean[N];
		
		powerset(0);
	}
	
	//메소드를 작성할때 최대한 파라미터를 심플하게 
	//idx : 해당 원소를 포함할지 안할지를 결정해야함.
	public static void powerset(int idx) {
		//base case : 재귀를 빠져 나갈 수 있는 조건
		//모든 재료를 넣을지 / 말지 에 대한 판단 끝났어!
		if(idx==N) {
			String tmp = "";
			for(int i = 0 ; i<N; i++) {
				if(sel[i])
					tmp+=재료[i];
			}
			System.out.println(tmp);
			return;
		}
		
		
		//recursive : 나 자신을 다시 호출하는 조건
		sel[idx] = true; //idx번째의 재료를 사용했어!
		powerset(idx+1); //다음 재료를 고려해~
		
		sel[idx] = false; //idx번째의 재료를 사용하지 않았어!
		powerset(idx+1); //다음 재료를 고려해~
	}
}
//
참치우엉삼겹살
참치우엉
참치삼겹살
참치
우엉삼겹살
우엉
삼겹살
(충무김밥)

 재귀를 이용한 부분조합

package day0321_부분집합_조합;

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;

public class 조합_1 {
	//재귀를 이용해서 조합을 만들어보자.
	static String[] 토핑 = {"상추", "패티", "토마토", "치즈"};
	static int N = 4;
	static int R = 2; // 문제에서 이런것들은 다 주어짐.
	
	static String[] sel = new String[R]; //내가 선택한 토픵
	
	static List<String[]> list = new ArrayList<>();
	
	public static void main(String[] args) {
		combination(0, 0);
		
		}
		
		

	//idx 	: 내가 이번 깊이에서 고려할 재료!
	//sidx  : 현재 뽑을 자리 
	public static void combination(int idx, int sidx) {
		//base case
		if(sidx == R) {//다 뽑았어
			System.out.println(Arrays.toString(sel));
			return;
		}
		//recursive case
		//경계값 결정
		for(int i = idx ; i<= N-R+sidx; i++) {
			sel[sidx] = 토핑[i];
			combination(i+1, sidx+1);
		}
	}
	
}
//
[상추, 패티]
[상추, 토마토]
[상추, 치즈]
[패티, 토마토]
[패티, 치즈]
[토마토, 치즈]

package day0321_부분집합_조합;

import java.util.Arrays;

public class 조합_2 {
	//재귀를 이용해서 조합을 만들어보자.
	static String[] 토핑 = {"상추", "패티", "토마토", "치즈"};
	static int N = 4;
	static int R = 2; // 문제에서 이런것들은 다 주어짐.
	
	static String[] sel = new String[R]; //내가 선택한 토픵
	
	public static void main(String[] args) {
		combination(0, 0);
		
	}
	//idx 	: 내가 이번 깊이에서 고려할 재료!
	//sidx  : 현재 뽑을 자리 
	public static void combination(int idx, int sidx) {
		//base case
		if(sidx == R) {//다 뽑았어
			System.out.println(Arrays.toString(sel));
			return;
		}
		if(idx == N) { //고려 다했어.
			return;
		}
		//recursive case
		sel[sidx] = 토핑[idx]; //sidx 자리에 현재 보고있는 idx 토핑을 저장할래
		combination(idx+1, sidx+1); //이번 재료 썼고, 다음재료 판단하러가보자.
		combination(idx+1, sidx);   //이번 재료 안썼고, 다음재료 판단하러가보자.
		
	}
	
}
//
[상추, 패티]
[상추, 토마토]
[상추, 치즈]
[패티, 토마토]
[패티, 치즈]
[토마토, 치즈]