공부방
 코딩 화이팅
코딩 화이팅
« 2025/04 »
| 일 |
월 |
화 |
수 |
목 |
금 |
토 |
| |
|
1 |
2 |
3 |
4 |
5 |
| 6 |
7 |
8 |
9 |
10 |
11 |
12 |
| 13 |
14 |
15 |
16 |
17 |
18 |
19 |
| 20 |
21 |
22 |
23 |
24 |
25 |
26 |
| 27 |
28 |
29 |
30 |
|
|
|
관리 메뉴
공부방
연약법과 귀납법, 수학적 귀납법 본문
CS/추론&논리회로
연약법과 귀납법, 수학적 귀납법
코딩 화이팅
2023. 7. 7. 11:19
추론
- 이미 "참"으로 알고 있는 명제(들)로 부터 새로운 "참"인 명제를 찾아내려고 한다. 이러한 과정을 통해서 새로운 지식을 덕게 된다.
- 올바른 추론의 규칙을 우리는 논리라고 부른다.
추론의 타당성
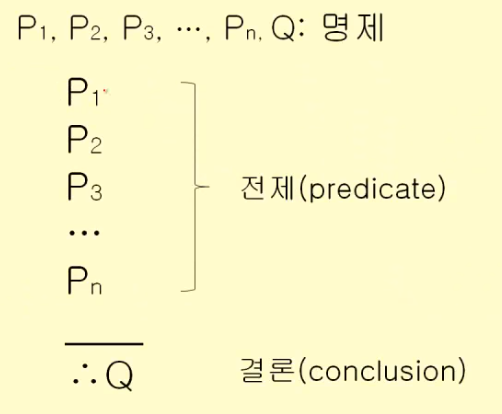
- P1, P2...들을 True라고 정해놓은것을 '전제'라고 한다.
- 새로운 명제를 찾아내려고 하는 것을 '결론'이라고 한다.
- 여기서 P들이 True라면 도출된 결론 Q는 True라고 주장할 때, 이 추론은 타당한가?
연역법
- 추론의 방법 중 하나
- 형식 논리의 다음과 같은 명제의 틀에 기반을 둔다.


연역법의 예
- 전제 : All men is mortal.(T)
Socrates is a man.(T)
- 결론 : Therefore, Socrates is mortal.(T)
- 전제 : 모든 컴퓨터 공학과 학생들은 C언어를 수강한다.(T)
김철수는 컴퓨터 공학과 학생이다.(T)
- 결론 : 그러므로 김철수는 C언어를 수강한다.(T)
- 전제 : 모든 농구 선수들은 키가 크다.(T)
김철수는 농구 선수이다.(T)
- 결론 : 그러므로 김철수는 키가 크다.(T)
귀납법
- 개별적인 사실을 말하는 명제들로부터 일반적인 결론을 도출하는 방법

귀납법 예
- 전제 : 김철수, 이영희, 홍복동은 컴퓨터공학과 학생이다.(T)
김철수는 c언어를 수강한다.(T)
이영희는 c언어를 수강한다.(T)
홍복동은 c언어를 수강한다.(T)
- 결론 : 따라서 모든 컴퓨터공학과 학생들은 c언어를 수강한다.(T?)
귀납법의 한계
- 귀납법의 문제는 현실적으로 집합의 모든 원소에 대해서 참인 것을 밝힐 수 없다는 점이다.
- 따라서 도출된 결론은 기껏해야 확률적인 결론일 수 밖에 없다.

수학적 귀납법
- 수학적 귀납법은 이러한 귀납법의 한계를 극복
- 집합의 모든 원소에 대해서 명제가 성립하는 것을 보여준다.
- 따라서, 모든 경우에 명제가 성립하는 것을 증명할 수 있다.

수학적 귀납법의 예















